Echelle spektroszkópia

Az echelle spektroszkópia

A Világegyetemben az információ túlnyomó része elektromágneses hullámok, kisebb hányada pedig részecskesugárzás formájában terjed. A megfigyelő csillagászat egyik legfőbb feladata a világűrből hozzánk érkező elektromágneses sugárzás megfelelő detektálása és a sugárzásban "kódolt" információ kinyerése, amely különböző feltevésekkel és modellekkel összevetve felvilágosítással szolgál a kibocsátó forrás, valamint a forrás és a megfigyelő közötti térrész természetéről, fizikai paramétereiről.

Az elektromágneses sugárzás hullámhosszától függően más és más észlelési és detektálási technika szükséges. A csillagászat egyik legfontosabb információgyűjtési technikája az objektumról hozzánk érkező elektromágneses sugárzás hullámhossz szerinti felbontása és az így nyert színkép későbbi feldolgozásra alkalmas rögzítése.

Echelle spektrográfokat az 1950-es évek elején történt első próbálkozások óta egyre nagyobb arányban használnak csillagászati célokra. Ennek oka, hogy ezen optikai rendszerek a hagyományos rácsos spektrográfokkal összehasonlítva sok, csillagászati szempontból fontos paraméter tekintetében messze túlszárnyalják azok teljesítményét úgy, hogy a hátrányok elhanyagolhatók ezen teljesítmény-növekedés előnyei mellett. A spektrográfokat mind földi, mind űreszközökre szerelt távcsöveken (pl. IUE) is sikerrel alkalmazzák.

Az echelle spektroszkópia alapegyenletei

A spektrográfok nevüket a bennük fő diszpergáló elemként alkalmazott ún. echelle rácsról kapták, ami egy nagy beesési és diffrakciós szöggel, magas interferencia-rendekben dolgozó, fűrészfog vagy lépcső alakú, speciális reflexiós rács.

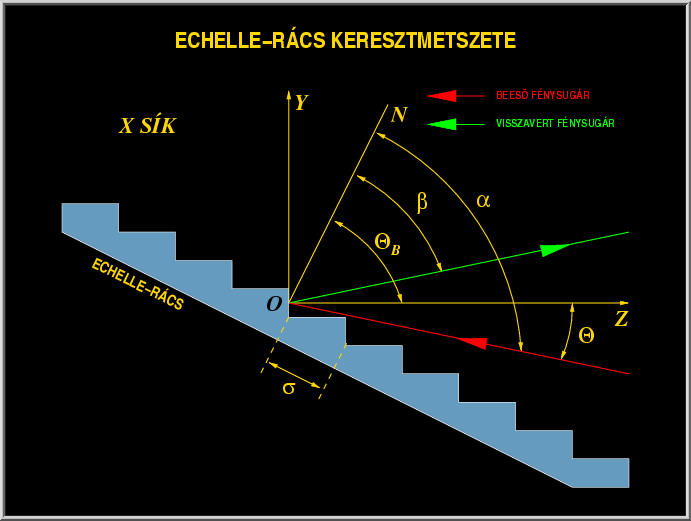
Echelle rács keresztmetszete.

A fenti ábra az echelle rácsnak egy, a "lépcsőkre" merőleges síkkal ($X = 0$) való metszetét és egy lokális koordináta-rendszert mutat. Az $Y$ tengely a fűrészfog hosszabbik, a $Z$ tengely a rövidebb élére merőleges. Az $ON$ félegyenes a rács, a $Z$ tengely pedig a lépcső normálisa. Az $\alpha$ a beesési szög, $\beta$ a diffrakciós szög, a $\Theta_B$ pedig az ún. ragyogási szög (blaze angle), az előbbiekben említett két normális szöge, $\sigma$ a rácsállandó. Az $\alpha$, $\beta$ és $\Theta_B$ szögeket általában nagyra, míg a $\Theta$ szöget (a beeső sugár és a $Z$ tengely szöge) kicsire választják. Jellemző értékek: $\Theta_B \sim 60^\circ$, $\Theta \sim$ néhány fok, $\sigma \sim 1/30 - 1/300$ mm.

Az ábra jelöléseit használva az echelle rács alapegyenlete a következő:

$\dfrac{m\lambda}{\sigma} = \cos \gamma \left [ \sin \alpha + \sin \beta(m) \right ]$,

ahol $m$ az az elhajlási rend, amelyik a $\lambda$ hulláhosszat tartalmazza, $\gamma$ pedig a beeső fénysugár és az $X = 0$ sík hajlásszöge. Könnyen látható, hogy a beesési és a visszaverődési szögekre az

$\alpha = \Theta_B + \Theta$, $\beta = \Theta_B - \Theta$

egyenletek írhatók fel, így a rácsegyenlet

$\dfrac{m\lambda}{\sigma} = 2 \cos \gamma \sin \Theta_B \cos \Theta$

alakú lesz.

Minden rendhez megadható az ún. centrális hullámhossz vagy ragyogási hullámhossz (blaze wavelength), amelynél az adott rendben az intenzitás a legnagyobb:

$\lambda_\text{c}(m) = \dfrac{2 \sigma \sin \Theta_B \cos \Theta}{m}$.

Konstans $\alpha$ beesési szög mellett az echelle rács szögdiszperziója:

$\dfrac{d\beta}{d\lambda} = \dfrac{m}{\sigma \cos \gamma \cos \beta} = \dfrac{2 \sin \Theta_B \cos \Theta}{\lambda \cos (\Theta_B - \Theta)}$.

Egy echelle elhajlási rend szögkiterjedése (angular spread) a

$\delta \beta = \dfrac{\lambda}{\sigma \cos \gamma \cos \beta} = \dfrac{2 \sin \Theta_B \cos \Theta}{m \cos \beta}$

formulával adható meg. Ha az echelle rendeket egy $f_2$ fókusztávolságú kamerával képezzük le, akkor a rend fókuszsíkbeli kitejedése (length of one order): $l = f_2 \delta \beta$.

Az ún. szabad spektrális tartomány (free spectral range) két egymást követő rendben az ugyanazon $\beta$ szögnél lévő hullámhosszak közötti különbség:

$\Delta \lambda = \lambda_{m+1} - \lambda_m = \dfrac{\lambda}{m} = \dfrac{\lambda^2}{2 \sigma \cos \gamma \sin \Theta_B \cos \Theta}$.

Minden $\lambda$ hullámhosszra létezik egy echelle rend, amelyben ez a hullámhossz $\Delta \lambda / 2$-nél nincs messzebb a rendere jellemző centrális hullámhossztól.

A spektrográf reciprok lineáris diszperziója (plate factor)

$P = \left ( f_2 \dfrac{d\beta}{d\lambda} \right )^{-1} = \dfrac{\sigma \cos \gamma \cos \beta}{m f_2} = \dfrac{\lambda \cos (\Theta_B - \Theta)}{2 f_2 \sin \Theta_B \cos \Theta}$.

Mivel az echelle spektrográfok magas rendekben dolgoznak, a szomszédos rendek közötti átfedés nagy, ezért szükséges a rendek térbeli szeparációja. Ez egy másik, ún. kereszt-diszperziós elemmel oldható meg, amelynek diszperziós iránya merőleges az echelle rács diszperziós irányára, s így a rendekre merőleges irányban szétválasztja azokat. Két egymás melletti rend detektorsíkbeli távolsága

$\Delta x = f_2 \delta \lambda \dfrac{d\beta^\prime}{d\lambda} = f_2 \delta \lambda \dfrac{m^\prime}{\sigma \cos \beta^\prime}$,

ahol a vesszős mennyiségek a kereszt-diszperziós elem jellemzői.

Legyen a spektrográf belépő résének szélessége $w$, $f_1$ pedig a kollimátor fókusztávolsága. Ekkor a belépő rés detektorsíkbeli mérete

$w^\prime = rw \dfrac{f_2}{f_1}$,

ahol az

$r = \dfrac{\cos \alpha}{\cos \beta} = \dfrac{d\beta}{d\alpha}$

egy projekciós faktor. Adott $f_2 / f_1$ mellett $r$-t 1-nél kisebbre kell választanunk, hogy a $w^\prime$ lehetőleg kicsi legyen. A spektrográf spektrális feloldó képessége definíció szerint

$\delta \lambda = w^\prime P = rw \left ( f_2 \dfrac{d\beta}{d\alpha} \right )^{-1}$,

ahol $\delta \lambda$ egy monokromatikus forrás effektív szélessége a fókuszsíkban. A spektrográf spektrális felbontása

$R = \dfrac{\lambda}{\delta \lambda} = \dfrac{2 f_1 \sin \Theta_B \cos \Theta}{w \cos \alpha}$.

Látható, hogy $R$ értéke csak $\alpha$-tól függ, $\beta$-tól nem. Bár a szögdiszperzió $\Theta = 0^\circ$ (ún. Littrow-elrendezés) esetén a legnagyobb, $R$ nem itt a maximális. $\Theta \sim 5^\circ$ esetén kb. 1.2-szer nagyobb, mint $\Theta = 0^\circ$ esetén.

Legyen $D$ a távcső, $d_1$ a kollimátor átmérője, $\psi$ pedig a belépő résnek megfelelő szögátmérő az égen. Ekkor

$R = \dfrac{d_1}{D \psi} \dfrac{2 \sin \Theta_B \cos \Theta}{\cos \alpha}$.

A Littrow-elrendezésben működő spektrográf esetén a szögdiszperzió csak a $\Theta_B$ szögtől függ. Egy hagyományos rács esetén $\Theta_B = 15^\circ$, azaz az echelle rács szögdiszperziója kb. egy nagyságrenddel jobb, így pl. a spektrum reciprok lineáris diszperziója a spektrográfot Cassegrain-fókuszban alkalmazva is elérheti azt az értéket, mint a Coudé-fókuszban elhelyezett hagyományos spektrográfok esetében. Azaz ugyanazon kollimátor-átmérő és belépő rés szélesség mellett jóval nagyobb spektrális felbontás érhető el, vagy ugyanolyan spektrális felbontás mellett az echelle spektrográfok sokkal érzékenyebbek.

Mivel a magas elhajlási rendek miatt a rendek közötti átfedés nagy, ezért szükség van egy ún. kereszt-diszperziós optikai elemre, ami a rendekre merőleges irányban széthúzza a spektrumot. Attól függően, hogy ezt a diszpergáló elemet az echelle rács előtt vagy utána helyezik el, pre-, ill. posztdiszperziós elemről beszélünk. A spektrográf által létrehozott színkép kétdimenziós lesz, ezért rögzítésére jól alkalmazhatók a modern kétdimenziós detektorok, régebben képerősítő csövek, manapság már főként CCD-kamerák. Bár a másodlagos diszpergáló elem fényveszteséget okoz, ezért azonban kárpótol az a tény, hogy az echelle spektrográffal a sok jelenlévő rend miatt nagy hullámhossz-tartomány fedhető le egy felvétellel, ezért alkalmazásával adott hosszúságú távcsőidő mellett jóval több információ gyűjthető össze a megfigyelt objektumról. Schroeder (1971) példája szerint egy 2-3 Å/mm reciprok lineáris diszperziójú echelle rács és egy 40 mm átmérőjű katóddal rendelkező képerősítő cső alkalmazása esetén az egy felvétellel lefedett színképtartomány kb. 2-3 ezer Å, míg ugyanezen csővel egy Coudé-spektrográf csak kb. 100 Å-t képes lefedni.

Mivel a Cassegrain-rendszerben kevesebb az optikai elem, mint a Coudé-rendszerben, ezért kevesebb a fényveszteség is, így akár 1^m nyereség is elérhető.

A teljesítmény további javítása

Az echelle spektrográfok fent vázolt jó tulajdonságai tovább javíthatók. Az egyik, hatásában legfontosabb változtatás a távcső és a spektrográf üvegszállal való összekötése. Ennek több előnye is van. Egyrészt elkerülhető a spektrográf belépő résének egyenetlen megvilágítása, mivel az üvegszál jól definiált pontszerű forrást biztosít. Másrészt a távcső és a spektrográf közötti üvegszálas kapcsolat lehetővé teszi, hogy a spektrográfot ne közvetlenül a távcsőre kelljen szerelni, hanem azt egy, a Coudé-szobához hasonló, esetleg légkondicionált, állandó feltételeket biztosító helyiségben helyezhessük el.

Az echelle spektrográfok a nagy diszperzió miatt igen érzékenyek a hőmérséklet- és pozícióváltozásból eredő mechanikai torzulásokra, ezért a távcsőre szerelt spektrográfok esetében nagy figyelmet kell fordítani arra, hogy a spektrumok redukálásához szükséges segédfelvételeket pontosan ugyanabban a távcsőpozícióban kell felvenni, mint a program objektum színképét, és közvetlenül előtte vagy utána, a deformációk ugyanis később hibát eredményezhetnek a hullámhossz-kalibrációban. Üvegszálas kapcsolat alkalmazása esetén ez a probléma nem merül fel a spektrográf fix elhelyezése miatt. Az üvegszál további előnye, hogy a Cassegrain-fókusz helyett a távcső primer fókuszába is elhelyezhető, így kiküszöbölhető a segédtükör zavaró hatása, s a kevesebb optikai elem miatt további foton-nyereség (kb. 10-20%) érhető el.

Az echelle spektrográfokban kereszt-diszperziós elemként alkalmazott optikai rácsok érzékenysége általában kicsi és az általuk okozott polarizáció nagy, ezért előnyösebb prizma használata kereszt-diszperziós elemként. Ezzel ismét 10-15 % foton-nyereség érhető el és az echelle rendek jobban szeparálhatók egymástól, ami fontos előny a feldolgozás során.

A feldolgozás módszere

Az echelle spektroszkópia az utóbbi évtizedek egyik legjobb észlelési technikája. A nagyméretű CCD-detektorok elterjedése lehetővé tette, hogy nagy spektrális felbontás mellett is egyszerre nagy hullámhossz-tartomány legyen lefedhető egyetlen felvétellel. Az adatfeldolgozás szempontjából azonban ennek a technikának is vannak hátrányai:

• A spektrumok nagy információsűrűsége és nagysága. Ez az utóbbi évek jelentős számítástechnikai fejlődése következtében egyre kevésbé probléma.

• Diszkontinuitások a rendeken belül.

• A szögdiszperzió rendről-rendre változik, s ez a változás több százalékot is kitehet.

• Nemcsak az egyes rendek intenzitása eltérő, hanem az a rendeken belül is változik (blaze function).

• A rendek közötti csökkenő távolság a rövidebb hullámhosszak felé.

• A CCD-mátrixoknak detektáló eszközként való alkalmazása is felvet néhány problémát, ezek elsősorban az expozíciós idő helyes megválasztásával függnek össze. A CCD-chipek egyik legnagyobb előnye, hogy dinamikus tartományuk hossza, azaz a "potenciálgödrök" elektrontároló kapacitása nagy, széles jelszint-tartományban lineáris választ adnak. Más detektorokhoz hasonlóan azonban ez a linearitás alacsony jelszint vagy túlexponálás esetén már nem áll fenn. Túl hosszú expozíciós idő esetén felléphet az ún. töltésáramlás jelensége, azaz egy adott pixelben el nem férő elektronok a szomszédos potenciálgödrökbe vándorolnak, meghamisítva az ott tárolt információt is. Ilyen módon a CCD egész oszlopai vagy sorai válhatnak használhatatlanná, ami esetünkben azért is rossz, mert az echelle spektrogramon a rendek nem pontosan párhuzamosak a CCD soraival, hanem kis szögben (kb. 5°) hajlanak azokhoz, így egy CCD-sor hibája esetleg több echelle rendet is befolyásolhat. A redukció során a rendek helyzetének könnyebb detektálása miatt az ilyen hibás sorokat célszerű a melletük lévő sorok számtani közepével helyettesíteni. Emiatt azonban az ott tárolt információ sérül, s erre később tekintettel kell lenni. Gondot okozhatnak még az ún. forró pixelek (hot pixels), azaz azok a hibás CCD-elemek, amelyek megvilágítás nélkül is teljesen telítettek. Az expozíciós időnek alsó korlátot szab a CCD kiolvasási zaja, felső korlátot az előbb említett tény, s az, hogy az expozíciós idő növelésével nő a becsapódó kozmikus részecskék nyomainak száma, amely egy 2 órás expozíció alatt a több százat is elérheti. Ezek kiszűrése megnehezíti, néha lehetetlenné teszi a megfelelő pontosságú továbblépést.

Az echelle spektrumok feldolgozásának igen jó eszköze a MIDAS (Munich Image Data Analysis System) programcsomagban implementált Echelle Reduction Package, amely egy jól struktúrált, de ugyanakkor flexibilis eszköz a különbözö echelle spektrográfokkal nyert spektrumok feldolgozásához.

A redukció tényleges megkezdése előtt a spektrumokat korrigálni kell néhány, már említett effektusra (a CCD rossz oszlopai, kozmikus részecskék nyomai). Ez utóbbiak eltávolítására a programcsomagban megfelelő parancsok állnak rendelkezésre, de a megmaradt nyomok is könnyen felismerhetők a redukció végén, ugyanis az egydimenziós spektrumban igen éles "emissziós" csúcsként jelentkeznek.

A redukció bevezető fázisának legfontosabb lépése a spektrum ún. standard állásba való forgatása, amikor is az egyes rendeken belül a hullámhossz balról jobbra, míg a rendek között lentről felfele nő, így a rácsegyenletnek megfelelően a rendek sorszáma lentről felfele csökken.

A feldolgozáshoz az objektum spektrumán kívül a következő segédfelvételek szükségesek:

• Egy, megfelelő számú és pontosan ismert hullámhosszú vonalakat tartalmazó színkép a hullámhossz-kalibrációhoz. Ez általában egy ThAr spektrállámpa spektruma.

• Egy ún. flat-field felvétel, ami egyrészt a spektrumot rögzítő CCD-kamera pixeleinek érzékenységéről nyújt információt, másrészt segítségével korrigálható az echelle rács által okozott, echelle rendeken belüli intenzitásváltozás. Erre a célra a legtöbb esetben a spektrográfba beépített magas hőmérsékletű izzólámpát használnak, vagy egy ilyen lámpával megvilágított fehér felület képét veszik fel, esetleg a szürkületi égbolt egy kis, egyenletes fényességű területének "színképét" rögzítik.

• Igen pontos redukciókhoz szükség van a CCD sötétáramának ismeretére, ami egy, az objektumról készült spektrum expozíciós idejével megegyező expozíciójú "vak" felvétellel vehető figyelembe.

• A CCD-pixelekben megvilágítás nélkül is jelenlévő "eltolási" elektronok által okozott hatás figyelembe vételére egy igen rövid expozíciójú (általában a kamerával végezhető legrövidebb expozíció), ún. "bias" felvételt is szoktak készíteni, s ezt levonják a többi képből.

• Ha a redukció végén abszolút intenzitáskalibrációt akarunk végrehajtani, akkor rögzíteni kell egy spektroszkópiai standard csillag spektrumát, aminek az intenzitáseloszlása a vizsgált hullámhossz-tartományban jól ismert. Ha csak ún. normált spektrumot akarunk kapni, ez a felvétel nem kell.

Nyers echelle spektrumok.
Nyers echelle spektrumok standard állásban. A rendek sorszáma alulról felfelé csökken, a hullámhossz a rendeken belül balról jobbra nő. A rendek kis szögben hajlanak a CCD soraihoz. Bal oldal: Objektum spektrum. A legfényesebb foltok a hidrogén Balmer-sorozatának tagjai, a Hβ, Hγ és a Hδ (fentről lefelé). A Hδ alatt egy hibás CCD-sor látható, aminek hatása a redukált spektrumon is megfigyelhető majd. A képen jól láthatók a kozmikus részecskék becsapódási nyomai is. Középen: Flat-field spektrum. Jobbra: ThAr spektrum a hullámhossz-kalibrációhoz.

A redukció lépései

1. A redukció első lépéseként a CCD-kamera által rögzített spektrum $(x, y)$ síkját transzformálnunk kell a $(\lambda, m)$ "térbe", azaz meg kell határoznunk az

   $y = f(x, m)$

   függvényt, ami az echelle rendek helyzetét definiálja, valamint a

   $\lambda = g(x, m)$

   összefüggést, ami a rendeken belüli diszperziós reláció. Előbbit az

   $y = f(x, m) \approx \sum\limits_{j=0}^J \sum\limits_{i=0}^I a_{ij} x^i m^j$

   kétváltozós, harmadfokúnál általában nem magasabb fokú polinommal, míg az utóbbit a

   $g = \lambda (x, m) = \dfrac{1}{m} \sum\limits_i^N a_i x^i$

   hatodfokú polinommal közelítjük. A kellő pontosság eléréséhez ezt a fázist egy kontrasztos felvételen, pl. a flat-field spektrumon célszerű végrehajtani, de az objektum spektruma is alkalmas lehet. Előfordulhat, hogy a hullámhossz-tartomány kék vége felé a flat-field felvételhez beépített izzólámpa intenzitása már kicsi, így itt a rendek néha nem különböztethetők meg jól a háttértől. Ekkor egy fényes csillag jól exponált spektrumát lehet (kell) használni.

   A polinomok együtthatói köztes táblázatokba kerülnek, s a további lépésekben a feldolgozó program a rendek helyzetének meghatározására ezeket a polinomokat használja. Ebben a fázisban történik még a rendek közötti gap-ek felmérése is a háttér későbbi levonása miatt. A pozíciók szintén táblázatba kerülnek.

   MIDAS parancs: define/echelle

2. A következő lépés a hullámhossz-kalibrációs spektrum (általában ThAr) vonalainak azonosítása, ill. a helyük megadása az $(x, y)$ síkban. Az eljárás kiindulásaként elegendő néhány vonal és az őket tartalmazó rend manuális azonosítása, a többi vonalat a feldolgozó program automatikusan detektálja. A program akkor fogad el egy vonalat helyesen azonosítottnak, ha a

   $\delta \lambda = \left | \lambda_\text{com} - \lambda_\text{cat} \right |$

   érték, ahol $\lambda_\text{com}$ a számított, $\lambda_\text{cat}$ pedig a táblázatbeli hullámhossz, kicsi a spektrum és a táblázat szomszédos vonalaiból képzetthez képest. A vonalazonosítás akkor tekinthető jónak, ha a fenti különbség összes vonalra képzett összege 10 mÅ-nél kisebb. Az azonosított vonalak $x$ és $y$ koordinátái, valamint a segédtáblázatokban adott laboratóriumi hullámhossza alapján felállítható a diszperziós reláció. Ha a kereszt-diszperziós elem rács és az egymást követő rendek átfedése akkora, hogy a vonal mindkét rendben megjelenik, akkor az automatikus vonalazonosítás kezdeteként elegendő csak két vonalat kijelölnünk.

   MIDAS parancs: calibrate/echelle

3. A rendek helyzetének felmérése és az összehasonlító spektrum vonalainak azonosítása után az első lépésben definiált pontokban meg kell határoznunk a spektrumokon a hátteret.

   MIDAS parancs: background/echelle

4. A háttér meghatározása után le kell vonnunk azt a spektrumokból. A parancs egyben a maradék kozmikus részecskéket is szűri.

   MIDAS parancs: filter/echelle

5. Következő lépésként egy olyan kétdimenziós képet kell elkészítenünk, amelynek sorai az echelle rendeket tartalmazzák. Például egy 260x337-es, 32 rendet tartalmazó CCD-képből így egy 260x32-es képet kapunk.

   MIDAS parancs: extract/echelle

6. A következő fázis igen kritikus a redukció szempontjából. Ez a kapott kétdimenziós kép két lépésből álló normálása:

   • Az echelle rács által okozott, rendeken belüli intenzitásváltozás (blaze function) simítása. A rendeken belüli intenzitásváltozás az

     $I(\lambda) = \dfrac{\sin^2 \pi \alpha X}{(\pi \alpha X)^2}$

     függvénnyel közelíthető, ahol $\alpha$ egy 0,5 és 1,0 közötti paraméter. $X = m (1 - \lambda_\text{c} (m) / \lambda)$ ($m$ a rend sorszáma, $\lambda_\text{c}$ pedig a centrális hullámhossza). A lépés elvégzése után az adott rendben egyre normált intenzitást kapunk.

     Ez a lépés elvégezhető a flat-field felvétel segítségével is (az objektum felvételét osztani kell a flat-field felvétellel), ez azonban egyes esetekben nem szolgáltat kellő pontosságot.

   • A kontinuum polinommal való illesztése.

7. A következő lépés az előző fázisban nyert kép (pixel, $m$) "térből" $(\lambda, m)$ "térbe" történő transzformálása, azaz a rendek hullámhossz szerinti átskálázása konstans lépésközzel.

   MIDAS parancs: rebin/echelle

8. A redukció utolsó két mozzanata a már hullámhosszban skálázott, de még különálló rendek összefűzése egyetlen egydimenziós spektrummá, s az így kapott egydimenziós színképnek a Föld heliocentrikus sebességére való korrekciója.

   MIDAS parancs: merge/echelle és compute/barycorr

A redukciós folyamat végén nyert egydimenziós spektrum már alkalmas a további analízisre, mérések elvégzésére.

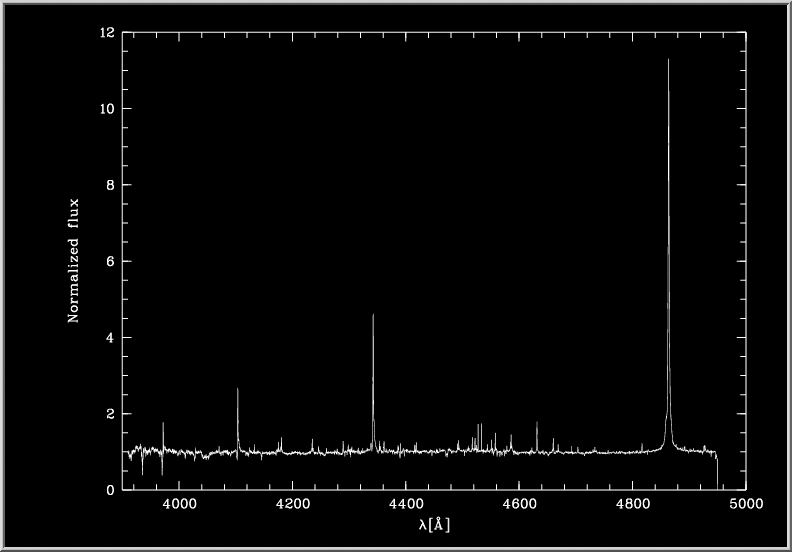
Egydimenziós spektrum.
Az echelle redukciós folyamat végén nyert egydimenziós spektrum. Az erős emissziós vonalak a hidrogén Balmer-sorozatának tagjai.

---

© 2002-2024 ELTE GAO MKK ♦ ☎ +36 94/522-870 ♦ obs@gothard.hu ♦ www.facebook.com/eltegao ♦ Oldaltérkép ♦ Impresszum